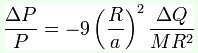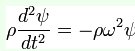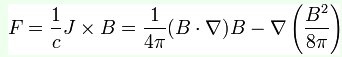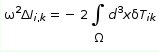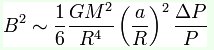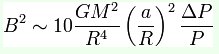Campi magnietici

Da Sezione Stelle Variabili - Unione Astrofili Italiani.

Qui di seguito presentiamo una trattazione semplificata del metodo usato da Applegate per discriminare i parametri delle stelle che hanno la peculiarità di presentare effetti magnetici rilevanti. E quindi vedremo le equazioni che collegano l'intensità superficiale del campo magnetico con le effettive variazioni di periodo orbitale.

Il problema per essere spiegato bene e per avere un' idea corretta, necessiterebbe di concetti un po' troppo complessi. Quindi mi limiterò a commentare qualche risulatato notevole. Iniziamo col presupposto che attività magnetiche molto intense (parecchi KG) generano due tipi di deformazioni nel sistema, o per meglio dire, nella stelle che generano lo stesso campo. Usando la stessa terminologia di Applegate:

• Deformazione per DISTORSIONE;
• Deformazione per TRANSIZIONE;

Il campo magnetico va ad agire sulla stella deformandola, se si deforma si hanno due effetti il primo è proprio questo delle distrosioni (la stella inizia a pulsare) il secondo tipo riguarda il fatto del cambiamento del quadripolo, a cui sussegue un cambio dell'oblatura e quindi inevitabilmente una ridistribuzione del momento angolare della stella. Partiamo dalle deformazioni:

in regime stazionario, una descrizione sensata della variazione del periodo orbitale è la seguente:

Come si può vedere delle eventuali variazioni di periodo sono legate al momento di quadrupolo Q , quindi per andare a evidenziare l'entità delle variazioni di periodo (quindi andare a valutare che effetto si ha sul diagramma O-C) basterà vedere come cambia il momento di inerzia della stella.

Mi metto nella condizione più semplice possibile: descrivo le pulsazioni con l'oscillatore armonico.

ora inizio a considerare l'azione della forza magnetica, riscivo le equazioni di Maxwell nel sistema CGS:

uso la legge di Lenz:

Ora per incollare il risultato che esce dalla legge di lez con le variazioni di periodo, sfrutto una piccola nozione di geometria. Riscrivo la forza agente su un fluido usando il tensore degli sforzi di Maxwell:

riprendo l eq dell'oscillatorie armonico e collego la forzante al campo magnetico:

Con conti abbastanza complicati e imponendo condizioni ben precise, si può definire anche la variazione del momento di inerzia. Il risultato è:

per chi fosse interessato i conti sono molto semplici, basta prendere la definizione usuale del momento di inerzia sostitutire la relazione tensoriale trovata tra il campo magnetico e la forza agente e poi integrare per parti e si arriva così al risultato scrtitto sopra. Effettuo l'integrazione e arrivo al risultato tanto sospirato !

Che rischivendo il tensore degli sforzi in funzione di B :

Quindi ora abbiamo la risposto al quesito iniziale: Come faccio a dinstinguere se la modulazione oscilloria del diagramma O-C è dovuta ad un terzo corpo o ad un effetto magnetico? Semplice, se consoco Raggio e Massa della stella e vedo che le variazioni di periodo si presentano in modo compatibile con l'equazione di campo scritta sopra allora posso portare delle valide ipotesi che supportano la tesi dell'effetto magnetico. Se l'equazione, fissati M ed R descrive un modello che non è compatibile allora la modulazione del diagramma O-C non è imputabile a cause magnetiche e quindi si cerca la motivaizone di tale oscillazione nella presenza di un terzo corpo o in altre cause. Ovviamente per rendere molto più semplice il lavoro del ricercatore sono state precompilate delle tabelle con tutti i dati di ampiezze del diagramma O-C in funzione alla classe spettrale delle componenti. Quindi si può avere subito un indice della correttezza del modello affidandosi a questi dati "preconfezionati". Sempre con le stesse considerazioni possiamo valutare anche l'effetto causato da una ridistribuzione del momento angolare dovuto dal cambio dell'oblatura della stella. I conti rispetto ai precedenti sono abbastanza semplici, infatti basta concentrarsi su come varia il quadripolo gravitazionale. Il collegamento al campo mangetico viene fatto imponendo che l'effetto di torsione di L sia puramente dovuto al campo in questione (cosa abbastanza vera). Alla fine otteniamo che :