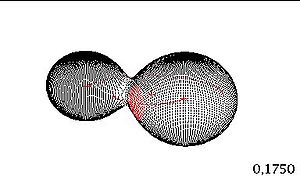
Introduzione EB
Da Sezione Stelle Variabili - Unione Astrofili Italiani.
Pensare agli oggetti del nostro cosmo come un qualcosa di eterno ed immobile è una concezione del tutto errata. Il nostro universo è in continua e inarrestabile evoluzione. La maggior parte di questi processi il cui effetto è macroscopico avviene su scale temporali molto grandi. Ci sono invece altri processi, la cui rilevazione è più complicata, che testimoniano la continua evoluzione del nostro cosmo. Gli oggetti più facili, che testimoniano questo, sono le così chiamate Stelle Variabili. Questo nome è associato proprio al fatto che sono particolari classi di stelle che variano la loro luminosità in tempi così brevi che è possibile rilevarne la variazione anche durante una singola serata osservativa. Esse si suddividono in variabili intrinseche cioè stelle che variano effettivamente la loro luminosità come le RR Lyr e le Cepheidi. Una seconda classe sono le variabili estrinseche cioè stelle che variano la loro luminosità per cause esterne. In questa pagina analizzeremo questo tipo di variabili e cercheremo di presentare eventuali processi e meccanismi che ne sono alla base.
Indice |
Tipologia di variabili estrinseche
Le cause per cui una stella varia estrinsecatamente la sua luminosità sono sostanzialmente due tra cui abbiamo:
- L'oggetto in analisi non è singolo ma è un sistema di due o più stelle che eclissandosi reciprocamente producono i cali di luminosità;
- Presenza attorno all'oggetto studiato di un disco di polveri ben localizzato o dalla densità variabile;
La prima tipologia di varianzione estrinseca della luce è molto diffusa. Moltissime stelle nell'universo si trovano aggregate in gruppi di tre o quattro componenti legate gravitazionalmente. La loro distanza può anche essere molto piccola, addirittura alcuni sistemi presentano componenti a contatto. La rotazione delle stelle intorno al baricentro comune avviene molto velocemente e l'effetto delle eclissi risulta visibile nell'arco anche di una sola sessione osservativa. Analizzando la forma della curva di luce (del calo di luminostià) si possono trarre molte considerazioni interessanti sui parametri fisici del sistema studiato. La seconda tipologia è molto più complicata, la forma della curva di luce è solitamente irregolare e dal Path è possibile ricostruire a spanne la grndezza e la densità del disco di polveri. Informazioni molto interessanti invece si hanno dall'analisi spettroscopica. Essendo il disco di polveri sostanzialmente freddo, questo assorbe la radiazione della stella. Da terra con spettroscopi ad alta risoluzione si elimina abbastanza facilmente (dal punto di vista concettuale, un po' meno da quello epistemologico) lo spettro della stella e si ha quindi una analisi spettrale del disco che fornisce importanti informazioni sulla sua natura chimica.
Di seguito vedremo che ci sono delle metodologie interessanti per poter tratte delle conclusioni spannometriche sui parametri fisici delle binarie ad Eclisse.
Sistema multiplo
Se due stelle sono disposte in modo tale che la loro inclinazione del piano orbitale permetta a noi dalla terra di osservare le reciproche eclissi, l'effetto di questo evento è banalmente rilevabile come un calo di luce. Ma se ci fosse una terza, quarta , quinta... componente che interagisce gravitazionalmente col sistema doppio eclissante, ma il suo piano orbitale ha un angolo tale che non entra nel gioco delle eclissi come facciamo a rilavarla ? (è sensato dire che l'angolo del piano orbitale potrebbe non far avvenire le eclissi del terzo corpo perchè, le due che si eclissano sono vicinissime mente la terza componente che noi stiamo cercando potrebbe essere molto distante e per fare una rivoluzione completa potrebbe impiegarci anni quindi il suo piano non è necessariamente allienato con quello delle due binarie eclissanti a cui è collegato). L'effetto di questa presenza è rilevabile dal diagramma O-C. Se questo diagramma mostra un pattern oscillatorio i cui parametri sono in accordo con i modelli fisici proposti, allora possiamo pensare che tale modulazione sia dovuta alla presenza di un terzo corpo. Infatti nella sua rivoluzione intorno al sistema doppio agisce con una specie di effetto di "marea" rallentando o velocizzando il moto delle binaire ad eclisse in funzione alla sua posizone. Dal diagramma O-C si possono estrarre dei parametri indicativi risolvendo le eq. differenziali del moto con la teoria della trasformata di fourier. Quindi tutto si riconduce ad interpolare il diagramma O-C con una serie di fuorier discreta e poi utilizzare i coefficienti di fourier per calcoalre i parametri di interesse:
Interpolo con:
<math> O-C = \frac{1}{2}a_0 + \sum_{k=1}^{2}\{a_ksin(k\omega E)+b_ksin(k\omega E)\}</math>
e ricavo che:
<math> e=\sqrt{\frac{a^2_2+b^2_2}{a^2_1+b^2_1}}</math>
<math> a\cdot sin(i)=c\cdot \sqrt{a^2_1+b^2_1}</math>
<math> f(m_3)= \frac{4\pi^2 a^3\cdot sin^3(i)}{G P^2}</math>
Scambi di massa
Là dove le componenti orbitanti hanno dimensioni maggiori del loro lobo di Roche, iniziano a perdere materia. Infatti la parte di materia che si trova oltre al potenziale critico è libero di lasciare la stella "madre" e quindi venir intrapplato dalla componente secondaria. Si ha quindi una corrente di massa dalla stella più massiva a quella meno massiva. Questo fatto ovvimente provoca una perdita di momento angorale che si ripercuote sul sistema doppio rallentandone sempre di più il periodo. Il tasso di rallentamento è costante perchè sostanzialemnte lo scambio di massa avviene con flusso costante, quindi abbiamo una tipica modulazione parabolica del diagramma O-C. I modelli più attendibili che sono oggi in uso, per cercare di simulare al meglio questi eventi sono bastati semplicemente sulle equazioni di Navier-Stokes. Infatti riscrivendo le equzioni dei fluidi per lo scambio di materia, si giunge facilmente ad una equzione differenziale che nonostante sia impossibile da risolvere in modo algebrico è relativamente facile ricostruire in modo numerico il comportamento in un intorno dei parametri iniziali fissati. Una particolare esponente di questo tipo di comportamementi è Algol. Tipica binaria ad eclisse dal periodo di circa 2 giorni. Su questa stella si ebbero notevoli problemi di interpretazione di evoluzione stellare, infatti non si capiva come la stella minore fosse evoluta in una subgigante ! Questo dato torno successivamente con l'interpretazione dei dati di O-C che descrivevano una nettisisma parabola. Quindi si inziò a proporre un modello di scambio di massa spiegando perchè la componente minore è evoluta in una subgigante.
Perticolari effetti mangetici
Essendo sistemi molto ravvicinati, le correnti superficiali che si possono innescare sono sorgenti di intenssissimi campi magnetici che vanno a modificare addiriuttara il periodo orbitale del sistema. Come sul nostro sole, anche le attività magnetiche che interessanto le altre stelle sono dei fenomeni periodici. Quindi l'azione che si presenta sarà anch'essa periodica e sarà visibile sul diagramma O-C. Infatti anche in questo caso il diagramma O-C avrà una modulziaone oscillatoria proprio perchè il fenomeno che agisce è periodico. Una domanda che sorge spontanea è la seguente: Quando siamo davanti ad un diagramma O-C con tipica modulazione oscillatoria, come facciamo a capire se questa è dovuta ad un terzo corpo o ad un effetto magnetico? Nelle prossime righe cercherò di spiegare come avviene questo tipo di discriminazione. Il problema per essere spiegato bene e per avere un' idea corretta, necessiterebbe di concetti un po' troppo complessi. Quindi mi limiterò a commentare qualche risulatato notevole. Iniziamo col presupposto che attività magnetiche molto intense (parecchi KG) generano due tipi di deformazioni nel sistema, o per meglio dire, nella stelle che generano lo stesso campo. Usando la stessa terminologia di Applegate:
- Deformazione per DISTORSIONE;
- Deformazione per TRANSIZIONE;
Il campo magnetico va ad agire sulla stella deformandola, se si deforma si hanno due effetti il primo è proprio questo delle distrosioni (la stella inizia a pulsare) il secondo tipo riguarda il fatto del cambiamento del quadripolo, a cui sussegue un cambio dell'oblatura e quindi inevitabilmente una ridistribuzione del momento angolare della stella. Partiamo dalle deformazioni:
in regime stazionario, una descrizione sensata della variazione del periodo orbitale è la seguente:
<math> \frac{\Delta P}{P} = -9\left(\frac{R}{a}\right)^2 \frac{\Delta Q}{MR^2} </math>
Come si può vedere delle eventuali variazioni di periodo sono legate al momento di quadrupolo Q , quindi per andare a evidenziare l'entità delle variazioni di periodo (quindi andare a valutare che effetto si ha sul diagramma O-C) basterà vedere come cambia il momento di inerzia della stella.
Mi metto nella condizione più semplice possibile: descrivo le pulsazioni con l'oscillatore armonico.
<math> \rho\frac{d^2\psi}{dt^2} = -\rho \omega^2 \psi </math>
ora inizio a considerare l'azione della forza magnetica, riscivo le equazioni di Maxwell nel sistema CGS:
<math> J = \frac{c}{4\pi}\nabla \times B </math>
uso la legge di Lenz:
<math> F = \frac{1}{c} J\times B = \frac{1}{4\pi}(B\cdot\nabla)B - \nabla\left(\frac{B^2}{8\pi}\right) </math>
Ora per incollare il risultato che esce dalla legge di lez con le variazioni di periodo, sfrutto una piccola nozione di geometria. Riscrivo la forza agente su un fluido usando il tensore degli sforzi di Maxwell:
<math> F_i = \nabla_i T_{ik} </math>
riprendo l eq dell'oscillatorie armonico e collego la forzante al campo magnetico:
<math> F_i = \nabla_i T_{ik} = \rho \omega^2 \psi_k</math>
Con conti abbastanza complicati e imponendo condizioni ben precise, si può definire anche la variazione del momento di inerzia. Il risultato è:
<math> \omega^2 \Delta I_{i,k} = -2\int_{\Omega}d^3x\delta T_{ik} </math>
per chi fosse interessato i conti sono molto semplici, basta prendere la definizione usuale del momento di inerzia sostitutire la relazione tensoriale trovata tra il campo magnetico e la forza agente e poi integrare per parti e si arriva così al risultato scrtitto sopra. Effettuo l'integrazione e arrivo al risultato tanto sospirato !
<math>\int_{\Omega}d^3x\delta T_{i,k} = \frac{1}{18} \omega^2 MR^2\left(\frac{a}{R}\right)^2 \frac{\Delta P}{P}</math>
Che rischivendo il tensore degli sforzi in funzione di B :
<math> B^2 \sim \frac{1}{6}\frac{GM^2}{R^4}\left(\frac{a}{R}\right)^2 \frac{\Delta P}{P}</math>
Quindi ora abbiamo la risposto al quesito iniziale: Come faccio a dinstinguere se la modulazione oscilloria del diagramma O-C è dovuta ad un terzo corpo o ad un effetto magnetico? Semplice, se consoco Raggio e Massa della stella e vedo che le variazioni di periodo si presentano in modo compatibile con l'equazione di campo scritta sopra allora posso portare delle valide ipotesi che supportano la tesi dell'effetto magnetico. Se l'equazione, fissati M ed R descrive un modello che non è compatibile allora la modulazione del diagramma O-C non è imputabile a cause magnetiche e quindi si cerca la motivaizone di tale oscillazione nella presenza di un terzo corpo o in altre cause. Ovviamente per rendere molto più semplice il lavoro del ricercatore sono state precompilate delle tabelle con tutti i dati di ampiezze del diagramma O-C in funzione alla classe spettrale delle componenti. Quindi si può avere subito un indice della correttezza del modello affidandosi a questi dati "preconfezionati". Sempre con le stesse considerazioni possiamo valutare anche l'effetto causato da una ridistribuzione del momento angolare dovuto dal cambio dell'oblatura della stella. I conti rispetto ai precedenti sono abbastanza semplici, infatti basta concentrarsi su come varia il quadripolo gravitazionale. Il collegamento al campo mangetico viene fatto imponendo che l'effetto di torsione di L sia puramente dovuto al campo in questione (cosa abbastanza vera). Alla fine otteniamo che :
<math>B^2 \sim 10\frac{GM^2}{R^4} \left(\frac{a}{R}\right)^2 \frac{\Delta P}{P}</math>