Introduzione EB
Da Sezione Stelle Variabili - Unione Astrofili Italiani.
(→Particolari Effetti) |
(→Particolari Effetti) |
||
| Riga 42: | Riga 42: | ||
<br> | <br> | ||
<br> | <br> | ||
| - | <br><br><br> | + | <br><br><br><br><br><br> |
== Bibliografia == | == Bibliografia == | ||
Versione delle 20:43, 26 set 2009
Pensare agli oggetti del nostro cosmo come un qualcosa di eterno ed immobile è una concezione del tutto errata. Il nostro universo è in continua e inarrestabile evoluzione. La maggior parte di questi processi il cui effetto è macroscopico avviene su scale temporali molto grandi. Ci sono invece altri processi, la cui rilevazione è più complicata, che testimoniano la continua evoluzione del nostro cosmo. Gli oggetti più facili, che testimoniano questo, sono le così chiamate Stelle Variabili. Questo nome è associato proprio al fatto che sono particolari classi di stelle che variano la loro luminosità in tempi così brevi che è possibile rilevarne la variazione anche durante una singola serata osservativa. Esse si suddividono in variabili intrinseche cioè stelle che variano effettivamente la loro luminosità come le RR Lyr e le Cepheidi. Una seconda classe sono le variabili estrinseche cioè stelle che variano la loro luminosità per cause esterne. In questa pagina analizzeremo questo tipo di variabili e cercheremo di presentare eventuali processi e meccanismi che ne sono alla base.
Indice |
Tipologia di variabili estrinseche
Le cause per cui una stella varia estrinsecatamente la sua luminosità sono sostanzialmente due tra cui abbiamo:
- L'oggetto in analisi non è singolo ma è un sistema di due o più stelle che eclissandosi reciprocamente producono i cali di luminosità;
- Presenza attorno all'oggetto studiato di un disco di polveri ben localizzato o dalla densità variabile;
La prima tipologia di varianzione estrinseca della luce è molto diffusa. Moltissime stelle nell'universo si trovano aggregate in gruppi di tre o quattro componenti legate gravitazionalmente. La loro distanza può anche essere molto piccola, addirittura alcuni sistemi presentano componenti a contatto. La rotazione delle stelle intorno al baricentro comune avviene molto velocemente e l'effetto delle eclissi risulta visibile nell'arco anche di una sola sessione osservativa. Analizzando la forma della curva di luce (del calo di luminostià) si possono trarre molte considerazioni interessanti sui parametri fisici del sistema studiato. La seconda tipologia è molto più complicata, la forma della curva di luce è solitamente irregolare e dal Path è possibile ricostruire a spanne la grndezza e la densità del disco di polveri. Informazioni molto interessanti invece si hanno dall'analisi spettroscopica. Essendo il disco di polveri sostanzialmente freddo, questo assorbe la radiazione della stella. Da terra con spettroscopi ad alta risoluzione si elimina abbastanza facilmente (dal punto di vista concettuale, un po' meno da quello epistemologico) lo spettro della stella e si ha quindi una analisi spettrale del disco che fornisce importanti informazioni sulla sua natura chimica. Di seguito vedremo che ci sono delle metodologie interessanti per poter tratte delle conclusioni spannometriche sui parametri fisici delle binarie ad Eclisse.
Sistema multiplo
Se due stelle sono disposte in modo tale che la loro inclinazione del piano orbitale permetta a noi dalla terra di osservare le reciproche eclissi, l'effetto di questo evento è banalmente rilevabile come un calo di luce. Ma se ci fosse una terza, quarta , quinta... componente che interagisce gravitazionalmente col sistema doppio eclissante, ma il suo piano orbitale ha un angolo tale che non entra nel gioco delle eclissi come facciamo a rilavarla ? (è sensato dire che l'angolo del piano orbitale potrebbe non far avvenire le eclissi del terzo corpo perchè, le due che si eclissano sono vicinissime mente la terza componente che noi stiamo cercando potrebbe essere molto distante e per fare una rivoluzione completa potrebbe impiegarci anni quindi il suo piano non è necessariamente allienato con quello delle due binarie eclissanti a cui è collegato). L'effetto di questa presenza è rilevabile dal diagramma O-C. Se questo diagramma mostra un pattern oscillatorio i cui parametri sono in accordo con i modelli fisici proposti, allora possiamo pensare che tale modulazione sia dovuta alla presenza di un terzo corpo. Infatti nella sua rivoluzione intorno al sistema doppio agisce con una specie di effetto di "marea" rallentando o velocizzando il moto delle binaire ad eclisse in funzione alla sua posizone. Dal diagramma O-C si possono estrarre dei parametri indicativi risolvendo le eq. differenziali del moto con la teoria della trasformata di fourier. Quindi tutto si riconduce ad interpolare il diagramma O-C con una serie di fuorier discreta. Il metodo matematico per determinare i pramatetri è quello proposto da Borkovitz-Hegedus nel 1996
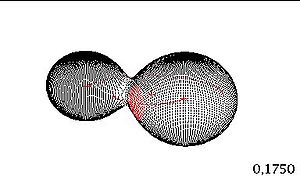
Scambi di massa
Là dove le componenti orbitanti hanno dimensioni maggiori del loro lobo di Roche, iniziano a perdere materia. Infatti la parte di materia che si trova oltre al potenziale critico è libero di lasciare la stella "madre" e quindi venir intrapplato dalla componente secondaria. Si ha quindi una corrente di massa dalla stella più massiva a quella meno massiva. Questo fatto ovvimente provoca una perdita di momento angorale che si ripercuote sul sistema doppio rallentandone sempre di più il periodo. Il tasso di rallentamento è costante perchè sostanzialemnte lo scambio di massa avviene con flusso costante, quindi abbiamo una tipica modulazione parabolica del diagramma O-C. I modelli più attendibili che sono oggi in uso, per cercare di simulare al meglio questi eventi sono bastati semplicemente sulle equazioni di Navier-Stokes. Infatti riscrivendo le equzioni dei fluidi per lo scambio di materia, si giunge facilmente ad una equzione differenziale che nonostante sia impossibile da risolvere in modo algebrico è relativamente facile ricostruire in modo numerico il comportamento in un intorno dei parametri iniziali fissati. Una particolare esponente di questo tipo di comportamementi è Algol. Tipica binaria ad eclisse dal periodo di circa 2 giorni. Su questa stella si ebbero notevoli problemi di interpretazione di evoluzione stellare, infatti non si capiva come la stella minore fosse evoluta in una subgigante ! Questo dato torno successivamente con l'interpretazione dei dati di O-C che descrivevano una nettisisma parabola. Quindi si inziò a proporre un modello di scambio di massa spiegando perchè la componente minore è evoluta in una subgigante.
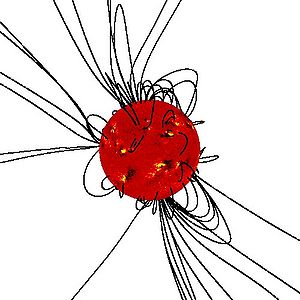
Perticolari effetti mangetici
Essendo sistemi molto ravvicinati, le correnti superficiali che si possono innescare sono sorgenti di intenssissimi campi magnetici che vanno a modificare addiriuttara il periodo orbitale del sistema. Come sul nostro sole, anche le attività magnetiche che interessanto le altre stelle sono dei fenomeni periodici. Quindi l'azione che si presenta sarà anch'essa periodica e sarà visibile sul diagramma O-C. Infatti anche in questo caso il diagramma O-C avrà una modulziaone oscillatoria proprio perchè il fenomeno che agisce è periodico. Una domanda che sorge spontanea è la seguente: Quando siamo davanti ad un diagramma O-C con tipica modulazione oscillatoria, come facciamo a capire se questa sia dovuta ad un terzo corpo o ad un effetto magnetico? La spiegazione non è molto semplice. Nel 1992 J.H. Applegate riuscì a descrivere in modo preciso la dinamica di questi effetti e quindi scrivere delle equazioni che mettessero in relazione il campo magnetico superciale con gli effetti di variazione del periodo. Le equazioni tengo conto anche dei parametri fisici della stella, quindi se nel fit dell'O-C tenendo fissi quei parametri vediamo che il modello non è compatibile allora di certo l'effetto oscillatorio in questione non è causato da campi magnetici, se invece tenedo i fissi i parametri che discendono dalla consocenza della classe spettrale della compente, il modello si adatta bene, allora possimao pensare che la moduzlazione in questione sia effettivamente causata da dei possibili campi magnetici. Per chi fosse interessato a capire bene la dinamica di questi particolari effetti rimandiamo alla seguente pagina: Campi magnetici
Particolari Effetti
Perticolari effetti che si possono rilevare sulle curve di luce di alcune tipiche binarie ad eclisse sono i seguenti:
Il primo riguarda le asimmetrie che si possono presentare sui massimi delle curve di luce. Le fasi di massimo della curva di luce indicano che in quell'istante le componenti del sistema binario in analisi sono appaiate rispetto alla nostra linea di vista. Da un punto di vista strettamente logico che siano appaiate con la componente primaria a destra e la secondaria a sinistra, o appaiate nel verso opposto non dovrebbe cambiare nulla, quindi ci si aspetterebbe che nella fase dei due massimi (il primo che si presenta dopo il minimo primario e il secondo che si presenta dopo il minimo secondario) la curva di luce abbia la stessa altezza indice del fatto che si raggiungono due intensità luminose identiche. Questo non è vero PER QUASI TUTTI i sistemi binari, infatti sono pochissimi i sistemi che non presentano questo effetto. Ovviamente su scale diverse, ma anche in lievissima parte, l'intesità lumonosa dei due massimi non è mai uguale. Un esempio è dato dall'immagine qui a lato raffigurante la stella CN And in cui questo effetto è particolarmente rilevante. Le cause fisiche che intervengono e provocano questi dislivelli, sono difficili da isolare. Studi fatti nel 1951 da O'Connell o anche i più recenti di Milone nel 1984 hanno cercato di spiegare questo effetto legando il dislivello di luminosità alla forma dell'orbita e alla forma delle componenti in analisi. Nonostante alcuni campioni presi in esame rispondessero in modo positivo al modello proposto, altre stelle che dal modello risultavano non essere affette dall'effetto di O'Connell invece lo presentavano. Questo punto fece sviluppare ulteriormente le ipotesi, fino a giungere ad un buona conclusione che è la seguente:
L'effetto di O'Connell è dovuto a parecche cause, la prima legata alla forma dell'orbita e delle componenti , la seconda invece alla presenza di ampie superfici di SUPERLUMINOSITA'. Il modello delle zone superluminose (o supercalde), chiamate anche HOT SPOT, viene presentato in un lavoro molto semplice ma geniale dai due astrofisici cinesi Qing-Yao Liu e Yu-Lan Yang, comparso su Chin.J Astronomy and Anstrophysics vol3 del 2003 N. 2, nelle pagine 142-150.
Il modello come detto in precedenza è molto semplice. Considerano le binarie strette come sistemi molto instabili. Fancendo questa ipotesi (del tutto lecita) viene subito da pensare che durante l'evoluzione del sistema un pochettino di gas degli stati più superficiali delle due componenti, oltrepassi di pochissimo il lobo di roche e quindi è ovvio pensare che questi sitemi molto perturbati siano sempre accompagnati da un alone. Le stelle ruotano all'interno di questo "alone" catturando materia. Supponendo che tutta la cattura di materia (quindi tutta l'enegia cinetica delle molecole di gas prese) venga tutta riconvertita in energia termica e quindi luminosa è facilissimo fare una stima della variazione di magnitudine bolometrica !!! Quindi se rispetto ad un nostro sistema di riferimento fissato le componenti ruotano in senso orario, avranno il mezzo emisfero che fa da fronte mediamente più luminoso dell'altro emisfero. Quindi si speiga molto banalmente le differenze di luce tra i due massimi. Con semplici conti è facile determinare anche la densità del disco di materia che circonda il sistema doppio. Tutti i conti sono fatti in dettaglio QUI.
Bibliografia
- En Applegate J.H. APJ 385:621-629,1992 Febbraio
- En David Bradstreet - Binary Maker: http://www.binarymaker.com/