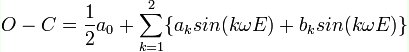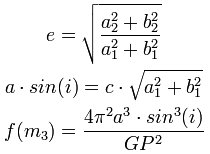Borkovitz-Hegedus nel 1996
Da Sezione Stelle Variabili - Unione Astrofili Italiani.
(Differenze fra le revisioni)
(Creata pagina con 'Dato il diagramma O-C oscillatorio, se da considerazioni preliminari che riguardano in specie l'esclusione di effetti magnetici, allora per estrerra i paratri del "possibile" ter...') |
|||
| (2 revisioni intermedie non mostrate.) | |||
| Riga 1: | Riga 1: | ||
| - | Dato il diagramma O-C oscillatorio, se da considerazioni preliminari che riguardano in specie l'esclusione di effetti magnetici, allora per estrerra i paratri del "possibile" terzo corpo dalla modulazione del diagramma O-C si sfrutta il modello proposto da Borkovitz T. e Hegedus T. nel 1996. I lttutto consiste nell'interpolare il diagramma O-C con una serie discreta di fourier: | + | Dato il diagramma O-C oscillatorio, se da considerazioni preliminari che riguardano in specie l'esclusione di [[Campi magnetici|effetti magnetici]], allora per estrerra i paratri del "possibile" terzo corpo dalla modulazione del diagramma O-C si sfrutta il modello proposto da Borkovitz T. e Hegedus T. nel 1996. I lttutto consiste nell'interpolare il diagramma O-C con una serie discreta di fourier: |
<center> | <center> | ||
[[File:inter1.jpg]] | [[File:inter1.jpg]] | ||
</center> | </center> | ||
| + | |||
| + | |||
| + | Usando i ciefficienti di fourier, e sfruttando la tecnica della risoluzioni delle eq. del modo con le trasformate di fuorier (Mth.di Kopal) si ottinene che i parametri del terzo corpo sono definiti come: | ||
| + | |||
| + | <center> | ||
| + | [[File:inter2.jpg]] | ||
| + | </center> | ||
| + | [[Category:Sezione EB - Binarie a eclisse]] | ||
Versione corrente delle 09:27, 20 set 2009
Dato il diagramma O-C oscillatorio, se da considerazioni preliminari che riguardano in specie l'esclusione di effetti magnetici, allora per estrerra i paratri del "possibile" terzo corpo dalla modulazione del diagramma O-C si sfrutta il modello proposto da Borkovitz T. e Hegedus T. nel 1996. I lttutto consiste nell'interpolare il diagramma O-C con una serie discreta di fourier:
Usando i ciefficienti di fourier, e sfruttando la tecnica della risoluzioni delle eq. del modo con le trasformate di fuorier (Mth.di Kopal) si ottinene che i parametri del terzo corpo sono definiti come: